Magnetization plateau in triangular lattice antiferromagnet

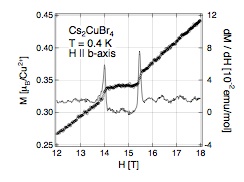
Phase diagram of Cs₂CuBr₄ in magnetic field is remarkably different from that of isostructural Cs₂CuCl₄: it has magnetization plateau at M= M_sat/3 (and another one, possibly, at M= 2 M_sat/3). Here M_sat is the magnetization of the fully polarized state.

Experimental data by T. Ono et al. Phys.Rev.B 67, 104431 (2003), J.Phys.:Condens. Matter 16, S773 (2004), Prog. Theor. Phys. Suppl. 159, 217 (2005). See also H. Tsuji et al., Phys.Rev.B 76, 060406 (2007).

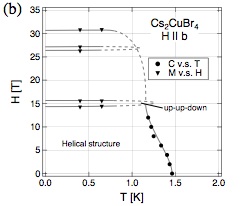
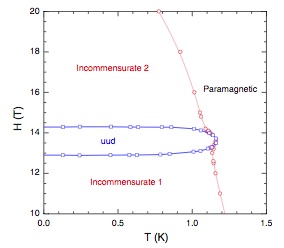
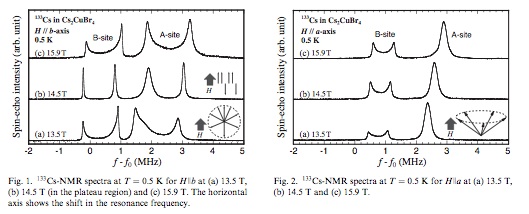
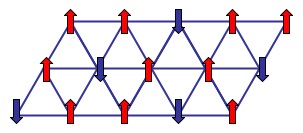
These as well as NMR measurements (Y. Fujii et al., Physica B 346-347, 45 (2004), JMMM 272-276, 861 (2004), J.Phys.:Condens. Matter 19, 145237 (2007)) indicate collinear UP-UP-DOWN (UUD) state, predicted by interacting spin wave calculations of A.V. Chubukov and D.I. Golosov, J.Phys.:Condens. Matter 3, 69 (1991). Closely related classical entropic mechanism has been analyzed by H. Kawamura and S. Miyashita, J. Phys. Soc. Jpn. 54, 4530 (1985).

One of the problems with this explanation is that its key element, UUD state, becomes classically unstable for arbitrary small spatial anisotropy in the exchange, that is when J'/J < 1. It is believed that Cs₂CuBr₄ has J'/J = 0.75 while Cs₂CuCl₄ has J'/J = 0.34.

The resolution is that quantum fluctuations can stabilize classical unstable state. This type of phenomena is known as "order-by-disorder". In our problem one needs to work with interacting spin waves from the very beginning, and treat spatial anisotropy (J - J') as a perturbation to the isotropic UUD state which is described by interacting spin waves. 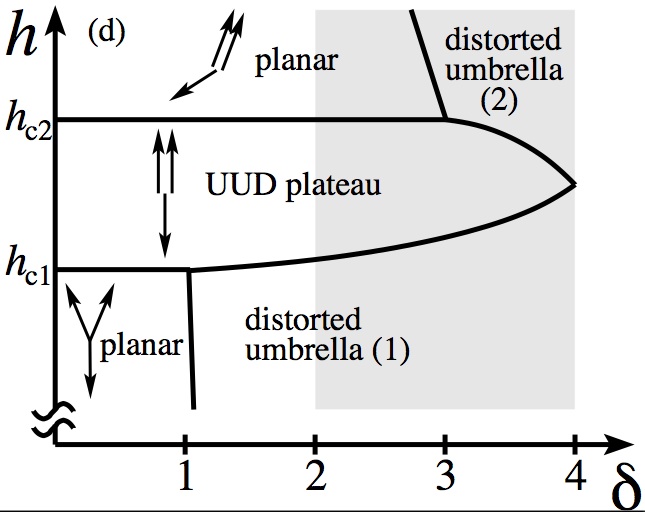It turns out that the competition between classical and quantum effects can be parametrized by a single dimensionless parameter δ=(40/3) S (J - J')²/J². The plateau is locally stable for 0 < δ < 4. However, it is a global minimum only for 0 < δ < 2. (It is interesting to note that δ=0.6 for Cs₂CuBr₄ while Cs₂CuCl₄ has δ=2.9.) This, and numerous BEC transitions out of the UUD state, are described in Quantum stabilization of the 1/3-magnetization plateau in Cs₂CuBr₄, Jason Alicea, Andrey V. Chubukov, and Oleg A. Starykh, Phys. Rev. Lett. 102, 137201 (2009).